El problema

Luces fuera es un juego de lógica en el que nos dan una tabla de luces que podemos apagar y encender. Cuando pulsamos el botón en una, se cambia el estado de esa luz y de todas las colindantes, y el objetivo es apagar todas. Os dejo un enlace a una versión gratuita y online que podéis jugar para echarle un ojo.

A lo largo de esta entrada voy a tratar el juego en su versión original con un tablero $5 \times 5$ . Si os gustan los juegos de puzzles, es probable que os hayáis topado con este juego o alguna de sus versiones anteriormente. En El Profesor Layton y la Llamada del Espectro podemos ver una versión $3\times 3$ del juego en el puzzle Sign Flipper, y otra versión $4 \times 4$ en Sixteen Tulips con el cambio de regla de que cada luz no cambia solo el estado de las colindantes sino de todas las celdas en su fila y su columna.

Sign Flipper Sixteen Tulips

Una versión incluso más graciosa, que ha sido la que me dio la idea para escribir esta entrada, es la que se encuentra en uno de los puzzles de Zero Escape: Zero Time Dilemma, curiosamente también sobre flores. En este caso cada flor afecta solo a ella misma y a las colindantes. Sin embargo, cada flor tiene tres estados (en lugar de dos como en el original) y la flor que pulsas cambia dos estados de golpe mientras que las colindantes solo uno.

Flores en ZTD

Cuando hice estos puzzles por primera vez normalmente suelo probar patrones simétricos, ya que producen resultados simétricos, que son los que normalmente nos piden, como en el ejemplo último de las flores. Sin embargo, estuve un tiempo considerable en el puzzle del Zero Time Dilemma (no sé si llegó a veinte minutos, pero tengo poca paciencia). Por lo que de la frustración llegó la idea de esta entrada. ¿Existe algún algoritmo sencillo que resuelva estos puzzles? ¿Y que lo resuelvan en el menor número de pulsaciones?

Sistema de ecuaciones

Pues sí, y estos algoritmos ya están inventados porque solo requiere resolver un sistema de ecuaciones lineales. De hecho, es fácil obtener el sistema inicial viendo el problema. Supongamos que queremos resolver el siguiente tablero (donde el naranja indica encendido, y el gris indica apagado):

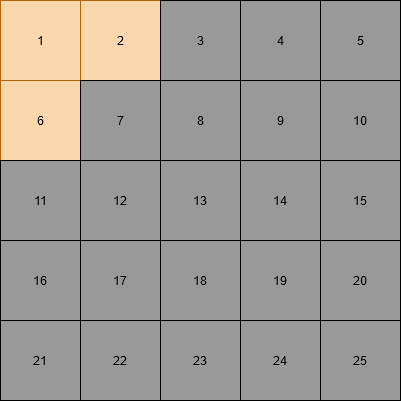
Esquema inicial

Es obvio que la solución con menos pulsaciones es clicar en la primera casilla. Pensemos ahora en qué sistema está asociado a este problema. Si denotamos $a_i$ a la variable asociada a pulsar o no el botón i-ésimo (bajo la enumeración de la imagen), con un $1$ si la pulsamos y un $0$ si no, todas las posibles combinaciones del vector de $25$ entradas cubren todos nuestros posibles inputs del juego, ya que pulsar dos veces un botón es lo mismo que no hacer nada. Esto nos da un espacio de $2^{25}$ posibles combinaciones, unas treinta millones.

En este caso, sabemos que $a_1 + a_2 + a_6 = 1$ (ojo que esta igualdad es en $F_2$ , el cuerpo finito con solo el $0$ y el $1$ ). Esto es debido a que queremos apagar la luz de la primera casilla, así que tendremos que pulsar un número impar de veces aquellas que cambian su estado. Si nos fijamos en una casilla que no queramos cambiar su estado, tendremos que pulsar un número par de veces las que la rodean. Por ejemplo, como la tercera casilla no la queremos ver afectada se tiene que $a_2 + a_3 + a_4 + a_8 = 0$ . De la misma forma se aplica para las $25$ casillas, y nos da un sistema de ecuaciones lineales en $F_2$ con $25$ ecuaciones e incógnitas.

Es más, sea $A$ la matriz de coeficientes de dicho sistema de ecuaciones, sea $x$ las variables (en este caso $(a_1, ..., a_{25}$ )) y sea $b$ el vector de los términos constantes, partiendo de la forma usual de los sistemas de ecuaciones lineales $Ax = b$ fijaos en que en cada posible puzzle de este tipo la matriz de coeficientes está fija, ya que solo depende de las reglas del puzzle: ¿qué celdas afectan a qué celdas y cómo lo hacen? Cuando nos dan la imagen a resolver, lo que nos están dando es $b$ , es decir los términos constantes. En el caso de arriba tendríamos como vector $b = (1, 1, 0, 0, 0, 1, 0, 0, ..., 0)$ .

Hay una pequeña pega al respecto. Porque, si bien ya podríamos resolver estos puzzles con un programa de unas pocas líneas que nos proporcione $x$ , a mano es algo complicado resolver un sistema de $25$ incógnitas, por mucho que estemos en $F_2$ donde algunas operaciones son más sencillas de lo habitual. De hecho, solo la matriz $A$ tiene $625$ términos. Así que necesitamos algún tipo de ayuda. En principio, nuestro caso ideal sería obtener un sistema sencillo de resolver. Por mucho que sean $25$ variables, si el sistema es triangular podríamos resolverlo paso a paso. Vamos a dejar esta idea aparcada un segundo para introduciros una técnica curiosa llamada perseguir las luces.

La técnica nace de que es posible resolver una fila tocando solo luces (o flores) de la fila de debajo. Solo tenemos que pulsar las celdas de debajo de las que están encendidas hasta apagarlas. Continuamos así hasta tener luces encendidas solo en la última fila. Aquí podéis ver un vídeo del tema. Después de esto, solo hace falta recordar tres patrones según que luces haya en la última fila y pulsar esos patrones en la primera fila, aplicando de nuevo el método para resolverlo entero. La pregunta es, ¿por qué funciona? ¿Por qué hay que recordar tres patrones, y no 32? Al fin y al cabo, hay un total de 32 combinaciones de luces encendidas en la última fila… ¿o no?

Volvamos a nuestra matriz $A$ de coeficientes del sistema de ecuaciones lineales. Los botones que pulsamos para perseguir las luces son los que van desde el número $6$ hasta el $25$ . Pensad un segundo en qué ocurre con la submatriz de las filas desde la $6$ hasta la $25$ . Voy a escribiros aquí parte de esta submatriz:

$\left(\begin{array}{cccccccc} 1 & 0 & 0 & 0 & 0 & 1 & 1 & \dots \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 & \dots \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & \dots \\ \end{array}\right)$

Si os lo estáis preguntando, la submatriz es triangular superior, no es difícil de probar. Lo cual permite, una vez que conocemos $b$ , resolver las primeras cuatro filas de la solución, que es lo que consigue perseguir las luces en la primera pasada.

Por otro lado, nos hemos dejado cinco ecuaciones, las cinco primeras. Si miramos el rango de $A$ comprobaremos que tiene rango $23$ , lo que significa que de hecho, solo nos hacen falta tres ecuaciones más, hay dos que no son necesarias. Lo que explica por qué solo necesitábamos tres patrones que recordar a la hora de la segunda pasada en perseguir las luces. Cada patrón se corresponde a una ecuación lineal, uno por si $a_{21}$ está activo tras la primera pasada, otro para $a_{22}$ y otro para $a_{23}$ . Si habéis visto el vídeo, de hecho son justo estos patrones los que se comentan.

Resolver el juego para otras versiones

Esto resuelve cómo conseguir resolver el juego de luces fuera con un algoritmo sencillo, solo tenemos que recordar tres patrones sencillos para la segunda pasada. ¿Cómo podemos usar esto a la hora de encontrar nuevas soluciones en diferentes versiones? En el caso de que cada celda afecte solo a las colindantes, la primera pasada será igual. Para la segunda necesitamos encontrar por nuestra cuenta nuevos patrones que nos sirvan a la hora de resolverlo. Los patrones son siempre iguales:

Clicar celdas en la primera fila.
Perseguir las luces hasta abajo.
Esto provoca un cambio solo en la última fila.
El número de patrones a conseguir es $rango(A) - (\text{número celdas}-\text{número celdas en una fila})$ . En el caso del $5\times 5$ era $23-(25-5) = 3$ . Como el rango lo desconocéis en general, no queda otra que suponer a base de los primeros patrones que hagáis. Otra opción es hacer todos los patrones posibles, que son $2^{\text{número celdas en una fila}}$ .

Tenemos que fijarnos en qué celdas clicamos, y qué celdas se cambian. Para el caso del $5\times 5$ original por ejemplo, los más sencillos son:

Celda 2 primera fila $\rightarrow$ Cambio en la $(1,2,3)$ de la última.
Celda 1 primera fila $\rightarrow$ Cambio en la $(2,3,5)$ de la última.
Celda 4 primera fila $\rightarrow$ Cambio en la $(3,4,5)$ de la última.

Mis recomendaciones: es mejor que los clics en la primera fila sean lo más sencillos posibles, probad primero solo un clic en solo una celda. Es necesario que los cambios en la última fila sean independientes. Esto os lo aseguráis siempre que la matriz sea triangular superior, en el caso del $5\times 5$ , sería:

$\left(\begin{array}{ccccc} 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ \end{array}\right)$

Básicamente, estamos intentando buscar una base de los vectores de estados del espacio que nos queda, que solo cambia estados en la última fila.

Solución óptima

Sin embargo, esto no responde totalmente a la pregunta de cómo calcular de antemano el menor número de pulsaciones para resolver el puzzle. Hay dos obstáculos bastante grandes:

Perseguir las luces tiene dos pasadas, y en ambas sabemos construir la solución paso a paso pero no de golpe. Si queremos construirla de antemano, necesitaríamos juntarlas desde el principio.
Aunque consiguiéramos esto, hay un problema fundamental. ¿Os acordáis de que la matriz $A$ tiene rango 23? Eso significa que cada puzzle tiene más de una solución. De hecho, hay exactamente cuatro soluciones por cada puzzle. Esto es señal simplemente de que hay dos vectores independientes $\{s_1, s_2\}$ tales que $As_1 = As_2 = 0$ . A continuación os dejo $s_1, s_2$ y $s_1+s_2$ .

esquema1 esquema2 esquema

Para resolver el primer problema podéis simular el algoritmo de perseguir las luces en una hoja en blanco, y tenéis que sumar las pulsaciones a las provocadas por los patrones de las celdas $2, 1$ y $4$ . Estas pulsaciones son:

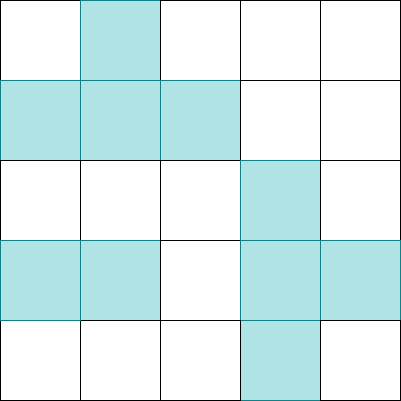
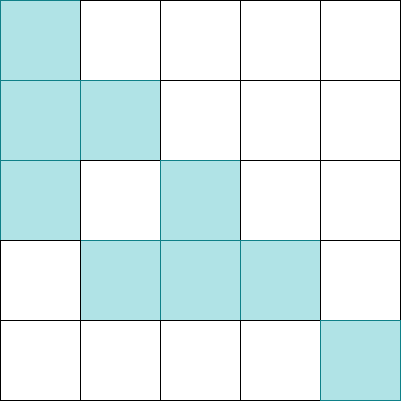
esquema1 esquema2 esquema

Si, por ejemplo, es necesario pulsar la celda 2 y 4 tendríais que hacer en una hoja de papel la suma de la simulación de perseguir las luces del original, la primera y la tercera imagen de las anteriores en azul. Esto produce una solución, llamémosla $s_0$ .

Ahora haría falta comprobar de las cuatro soluciones posibles $\{s_0, s_0+s_1, s_0+s_2, s_0+s_1+s_2\}$ cuál es la que tiene menos pulsaciones, con las imágenes que he colocado antes en rojo. Gracias a que estos patrones son simétricos son un poco más fáciles de recordar.

Como es razonable, estas soluciones y patrones no se pueden obtener en versiones generales del juego sin un ordenador por delante. Si bien los patrones azules que aparecen de la segunda pasada de perseguir las luces se pueden obtener simplemente anotando qué pulsamos en cada uno de ellos, para conseguir $s_1, s_2$ es necesario saber el rango de $A$ y resolver el sistema de ecuaciones, por lo que al final estamos donde empezamos. Si en algún otro juego me piden hallar la solución óptima, y necesito algún algoritmo para resolverlo en menos de veinte minutos sin frustrarme quizá continúe la búsqueda, pero por hoy creo que me quedo satisfecho.