Explicando con detalle: demostración del Teorema de Holditch

Uno de mis principales defectos en matemáticas es que tiendo a olvidarme de los detalles de las demostraciones que leo. Una forma sencilla de resolver esto es escribir las demostraciones con el nivel de detalle que nos satisfaga, para poder tener una referencia a la hora de recordar los resultados. Hoy voy a hacer esto con un teorema que siempre me ha impactado: el teorema de Holditch.

El teorema tiene una demostración cortísima que podéis ver en este artículo de Arne Broman. De hecho, la demostración del propio Holditch en 1858 es media página, aunque como se detalla en el artículo de Broman, hay bastantes suposiciones implícitas en los cálculos. Además, no es solo corta, si no que es realmente simple conociendo con anterioridad el teorema de Green o el teorema de la divergencia. Así que, ¿qué necesidad hay de reescribir esta demostración?

El problema recae en que cuando vi la demostración con notación moderna, tuve varios problemas en entender un paso en concreto. Para cualquier persona que entienda de formas diferenciales o que tenga una comprensión profunda (más allá de definirlo como un símbolo que denota bajo qué variable integramos) de la notación del diferencial $d$ en las integrales de curvas y superficies, es probable que este post le parezca una pérdida de tiempo, y le instaría a leerse la demostración de Broman que he enlazado anteriormente. Mi intento aquí va a ser traducir la demostración a una notación que me es más cómoda.

Comentado los objetivos, vamos con el teorema en sí. La idea que se intenta formalizar es la de un segmento de longitud fija $a+b$ con los extremos en una curva $C$ del plano. Si nos fijamos en la curva trazada por el punto que separa la curva en otras dos de longitud $a$ y $b$, el teorema afirma que el área entre $C$ y esta nueva curva es exactamente $\pi a b$. Lo que más resalta de este resultado es que no depende de la curva $C$ en absoluto. En la imagen de abajo podéis ver un boceto de las definiciones básicas del teorema, donde el área que mide $\pi a b$ sería la que se queda entre $C$ y la trazada por $\delta(t)$. Aquí podéis ver varios ejemplos de gifs animando el proceso de obtener una curva de esta forma, están graciosos. Vamos a formalizarlo.

---

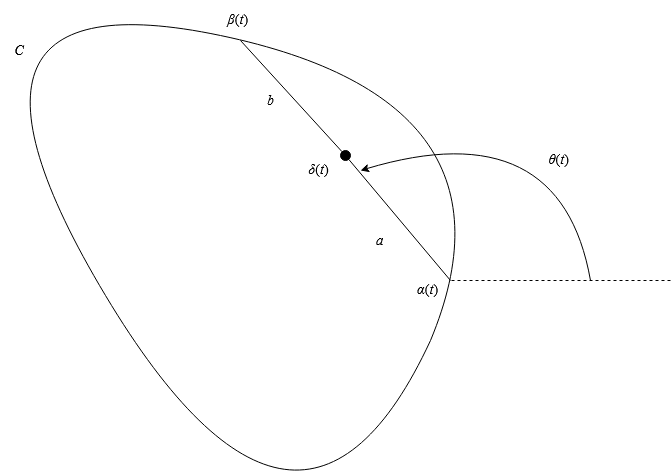
Teorema de Holditch: Partimos de una curva $C$ simple, cerrada y convexa. Sean $\alpha, \beta:[0,1]\rightarrow C$ dos curvas que recorren $C$ en sentido anti-horario, tales que el segmento $[\alpha(t),\beta(t)]$ es una cuerda de longitud fija $a+b$ para todo $t\in [0,1]$, y cumpliendo que son inyectivas salvo en $t=0$ y $t=1$ donde $\alpha(0) = \alpha(1)$ y $\beta(0) = \beta(1)$, habiendo completado una vuelta exacta sobre $C$. Para cada $t\in [0,1]$ existe un punto $D_t$ de la cuerda entre $\alpha(t)$ y $\beta(t)$ tal que el segmento $\overline{\alpha(t)D_t}$ tiene longitud $a$ y el segmento $\overline{D_t\beta(t)}$ tiene longitud $b$. Definimos $\delta:[0,1]\rightarrow \mathbb{R}^2$ como $\delta(t) = D_t$.

Sea $\{e_1, e_2\}$ la base usual del plano, definimos para cada $t\in[0,1]$ $\theta(t)$ como el ángulo entre $e_1$ y $\beta(t)-\alpha(t)$ en sentido anti-horario, empezando la orientación desde $e_1$, por lo que $\theta$ es una función con imagen contenida en $[0,2\pi)$. Es más, siendo $\theta$ una función continua con dominio $[0,1]$ y rango $[0,2\pi]$ con una relación de equivalencia entre $0$ y $2\pi$, por lo que este conjunto es homeomorfo a $\mathbb{S}^1$. Fijando $T = \theta(0)$ sabemos que existe un único levantamiento $\tilde{\theta}:[0,1] \rightarrow \mathbb{R}$ de $\theta$ y con $\tilde{\theta}(0) = T$. Necesitamos el levantamiento para tratar con una función continua. Si no tenemos cuidado, $\theta$ será continua en el espacio cociente de los ángulos de $[0,2\pi]$ bajo la equivalencia de los extremos, pero no como función de variable real. Se usará $\theta$ como el levantamiento, no como su definición original. De esta forma, $\theta(1) = \theta(0)+2\pi$ y $\theta$ es continua como función de variable real. Bajo todas estas premisas, si $\theta$ es monótona creciente y $\delta$ es una curva simple cerrada, entonces el área entre $C$ y la curva delimitada por $\delta$ es exactamente $\pi a b$.

---

El enunciado del teorema es largo en parte porque he querido ser explícito en la definición de $\theta$. En el artículo que enlazo esta definición se deja en base a un simple esquema, dejando implícita la parte de que cuando $\beta(t)-\alpha(t)$ completan una vuelta y es igual a $e_1$, el ángulo no vuelve a cero, si no que continúa incrementando desde $2\pi$. No he visto forma de formalizar esto aparte de usar la teoría de levantamiento de funciones.

La demostración va a necesitar el teorema de la divergencia del plano, así que lo voy a enunciar a continuación:

---

Teorema de la divergencia en el plano: Sea $S$ un conjunto compacto y conexo del plano con borde $C$ diferenciable. Sea $\nu:C\rightarrow \mathbb{R}^2$ definiendo $\nu(p)$ como el normal a $T_pC$ cuyo sentido viene dado por la dirección que apunta hacia $S$ (cuyo interior está bien definido por el teorema de la Curva de Jordan). Sea $X:S\rightarrow \mathbb{R}^2$ un campo diferenciable. Entonces: $\int_S \text{div} X = -\int_C \langle X, \nu \rangle$

---

Y con todo esto, ya tenemos todas las partes necesarias para hacer la demostración del teorema.

---

Demostración del teorema de Holditch: Sea $S$ la región delimitada por $C$, es un conjunto compacto y conexo por ser $C$ una curva simple y cerrada. Sea $X(x,y) = (x,0)$, es un campo diferenciable así que podemos aplicar el teorema de la divergencia. En este caso, $\text{div} X = 1$ así que:

$$A(S) = \int_S 1 = \int_S \text{div} X =- \int_C \langle X, \nu \rangle.$$

Para integrar en $C$ nos hace falta una curva que la parametrice, pero podemos usar las expresiones de $\alpha$ y $\beta$ debido a que recorrían $C$. Sea $S_\delta$ la región delimitada por la curva $\delta$. Nuestro objetivo es probar que $A(S)-A(S_\delta) = \pi a b$ (nótese que sabemos que $S_\delta \subset S$ ya que $D_t\in S$ para todo $t$ por la convexidad de $C$). Así que aplicamos el teorema de la divergencia a $S_\delta$ y obtenemos:

$$A(S_\delta) = \int_{S_\delta} 1 = \int_S \text{div} X = - \int_D \langle (x,0), \nu \rangle,$$

siendo $D$ la curva trazada por $\delta$. Volviendo a $A(S)$, podemos aplicar que $\beta(t)$ es una parametrización y que, además, $\beta(t) = \delta(t) + b(\cos(\theta(t)), \sin(\theta(t)))$ ya que recordemos que el segmento que unía $\alpha(t), \delta(t)$ y $\beta(t)$ tenía dirección $\theta$ y la distancia entre $\delta$ y los otros dos puntos estaba fija a $a$ y a $b$. De esta forma, tenemos:

$$A(S) = - \int_C \langle (x,0), \nu \rangle = -\int_0^1 \langle X(\beta(t)), \nu(\beta(t))\rangle dt$$

Pensemos un segundo que si $\beta(t) = (\beta_1(t), \beta_2(t))$ entonces $X(\beta(t)) = \beta_1(t)$ y $\nu(\beta(t)) = (-\beta_2'(t), \beta_1'(t))$. En efecto, $T_{\beta(t)}C$ viene definido por el tangente $\beta'(t) = (\beta_1'(t), \beta_2'(t))$, por lo que el $\nu$ que era normal a $T_{\beta(t)}C$ es proporcional a $(-\beta_2'(t), \beta_1'(t))$. Como $\beta$ recorría $C$ en sentido anti-horario, tenemos que $\nu$, definido como aquel normal que apunta hacia $S$, debe ser un giro de $\pi/2$ en sentido anti-horario, definido por la matriz $\left(\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right)$, dejándonos $\nu(\beta(t)) = (-\beta_2'(t), \beta_1'(t))$. Así que obtenemos:

$$A(S) = \int_0^1 \beta_1(t)\beta_2'(t)dt = \int_0^1 (\delta_1(t)+b\cos(\theta(t))) (\delta_2'(t) + b \cos(\theta(t)) \theta'(t))dt,$$

donde recordemos que $\theta$ era monótona creciente por lo que el conjunto de puntos donde no es diferenciable es de medida cero y no tenemos ningún problema derivando en $\delta$. Aplicamos propiedad distributiva y agrupamos:

$$A(S) = \int_0^1 \delta_1(t) \delta_2'(t) dt + b\int_0^1 \delta_2'(t)\cos(\theta(t)) + \delta_1(t)\cos(\theta(t))\theta'(t)dt + b^2\int_0^1 \cos(\theta(t))^2 \theta'(t)dt.$$

Por otro lado, el mismo proceso se puede hacer empezando la parametrización por $\alpha$ y recordando que $\alpha(t) = \delta(t) - a(\cos(\theta(t)), \sin(\theta(t)))$:

$$A(S) = \int_0^1 \alpha_1(t) \alpha_2'(t) dt = \int_0^1 (\delta_1(t)-a\cos(\theta(t))) (\delta_2'(t) -a \cos(\theta(t)) \theta'(t))dt,$$ $$A(S) = \int_0^1 \delta_1(t) \delta_2'(t) dt -a\int_0^1 \delta_2'(t)\cos(\theta(t)) + \delta_1(t)\cos(\theta(t))\theta'(t)dt + a^2\int_0^1 \cos(\theta(t))^2 \theta'(t)dt.$$

Multiplicando la primera ecuación, con $\beta$, por $a$, multiplicando la segunda ecuación, con $\alpha$, por $b$ y sumando ambas, nos queda:

$$(a+b)A(S) = (a+b)\int_0^1 \delta_1(t) \delta_2'(t)dt +ab(a+b)\int_0^1 \cos(\theta(t))^2 \theta'(t)dt.$$

Es importante notar que, exactamente de la misma forma que usamos el teorema de la divergencia para $A(S_\delta)$, si continuamos veremos que este área es igual a $\int_0^1 \delta_1(t) \delta_2'(t)dt$, la integral de la ecuación. Para finalizar, nótese que el integrando de la última integral es la derivada de otra función (la integral de coseno cuadrado compuesta con la propia $\theta$): $g(t) = (\theta(t)+\sin(\theta(t))\cos(\theta(t)))/2$. En efecto:

$$g'(t) = (\theta'(t) + \cos(\theta(t))^2\theta'(t) - \sin(\theta(t))^2\theta'(t))/2 = \theta'(t)(1-\sin(\theta(t))^2+\cos(\theta(t))^2)/2 = \theta'(t)\cos(\theta(t))^2.$$

Finalizamos viendo que utilizando que $\theta(1) = \theta(0)+2\pi$ tenemos $g(1)-g(0) = \pi$. Sustituyendo en la expresión anterior, nos queda:

$$(a+b)A(S) = (a+b)A(S_\delta) +ab(a+b)\pi.$$

Dividimos por $(a+b) > 0$ y tenemos:

$$A(S) - A(S_\delta) = \pi a b.$$

---

Y así finaliza el teorema de Holditch. Si has llegado hasta aquí espero que te haya sido de ayuda. Un saludo.