Tomar el límite de una sucesión de funciones por sus gráficas

Normalmente cuando se estudian sucesiones de funciones $f_n:A \rightarrow \mathbb{R}$, con $A\subset \mathbb{R}$, se suelen estudiar la convergencia punto a punto y la convergencia uniforme. Ambos conceptos son bastante naturales, y de hecho tienen una interpretación geométrica muy sencilla. El límite punto a punto es simplemente repetir el proceso de convergencia que ya se crea en sucesiones $a_n$ de números reales. A mí me gusta imaginar que para cada punto aparecen dos ventanas negras gigantes impidiéndote ver el resto, ya que solo te importa la sucesión del único punto que puedes ver.

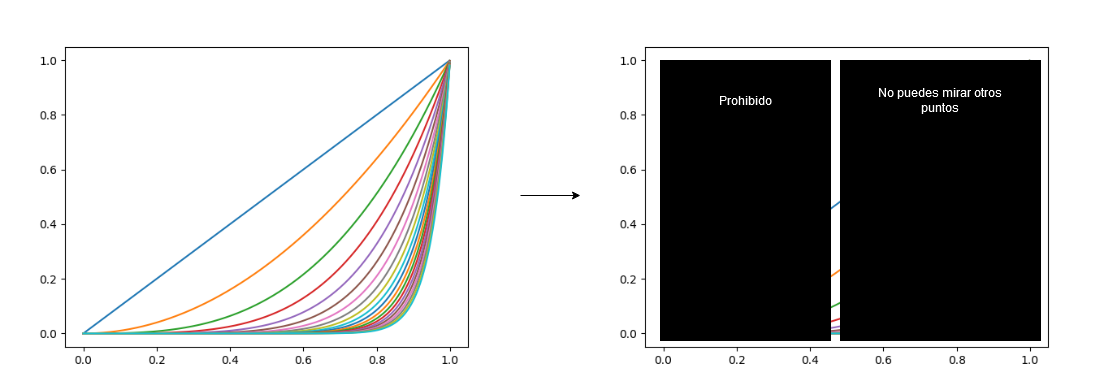
Por otro lado, la convergencia uniforme es equivalente con la pregunta: ¿puedo aplastar la sucesión en su límite o no? Esta visualización viene de que $f_n$ converge uniformemente a $f$ si y solo si $\sup \vert f_n - f\vert \rightarrow 0$. Por ejemplo, si $f_n(x) = \frac{\sin(x)}{n}$, sabemos que converge uniformemente a $f=0$, y podemos ver que efectivamente la función $f_n-0$ se aplasta entre su máximo y su mínimo:

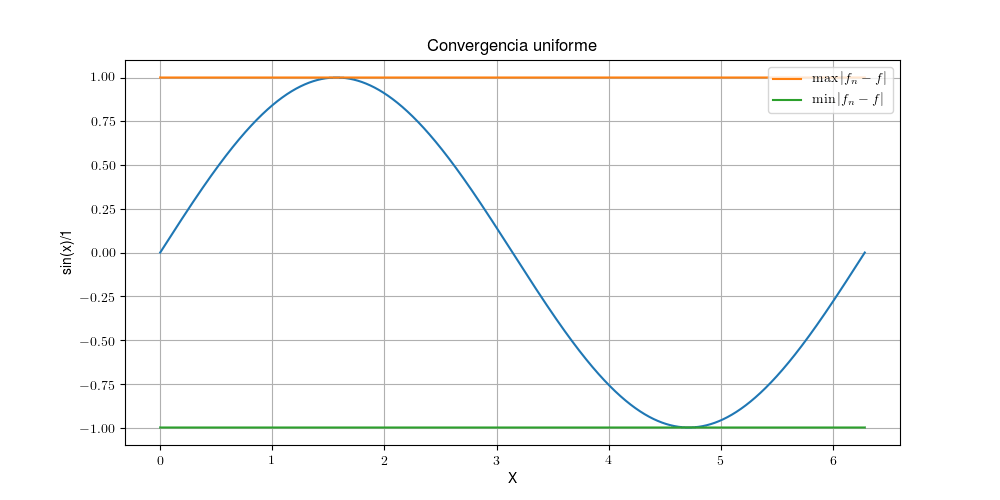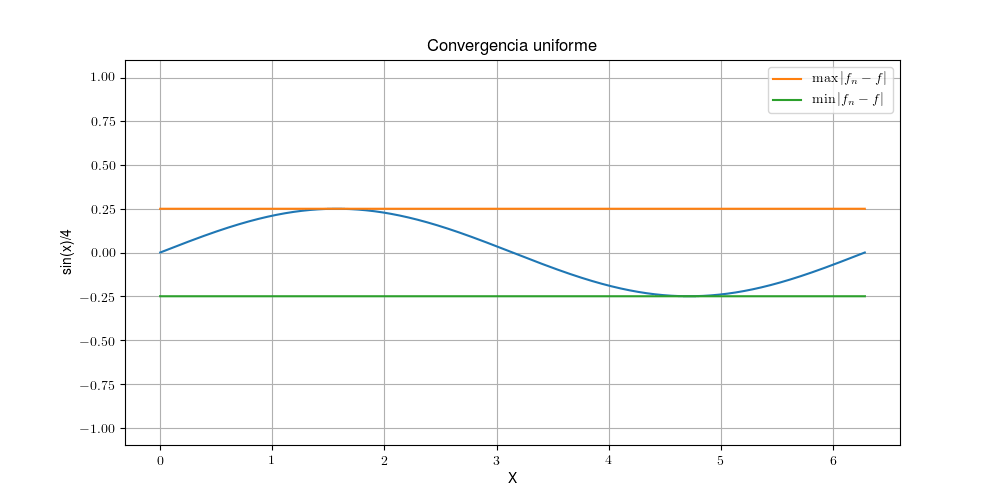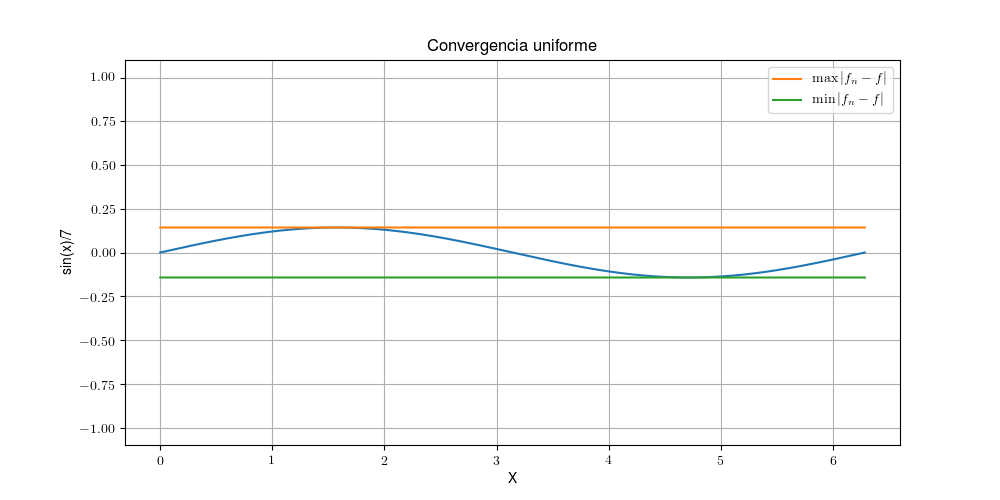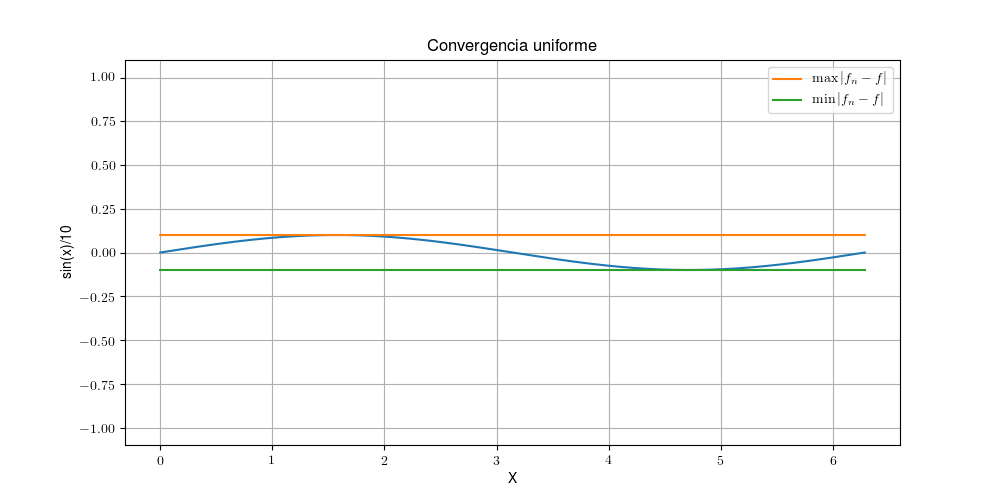
Si intentáramos hacer esta prueba en la sucesión anterior, el máximo se nos queda atascado en la recta $y=1$ y no llega nunca a bajar. Así que tenemos dos maravillosos límites de sucesiones de funciones, vamos a intentar definir uno nuevo.

Las gráficas de las funciones $f_n : A\rightarrow \mathbb{R}$, cuando $A$ es un conjunto compacto de $\mathbb{R}$ y $f_n$ son continuas, son conjuntos compactos de $\mathbb{R}^2$. Existe una distancia en estos conjuntos que lo convierte en un espacio métrico, la distancia de Hausdorff. La definición de esta distancia es:

$$d_H(X,Y) := \max \{ \sup_{x\in X} d(x,Y), \sup_{y\in Y} d(X,y) \},$$

donde se usa que $d(x,Y) = \inf_{y\in Y} d(x,y)$. El significado de la distancia es ‘La máxima distancia desde alguno de los puntos al otro conjunto’. La demostración de que forma una métrica en el conjunto de compactos de $\mathbb{R}^2$ es sencilla, el único detalle algo más largo de demostrar sería la desigualdad triangular. La demostración la podéis ver en el Teorema 3.1 aquí.

Aunque parezca algo complicada, los límites son bastante intuitivos. Por poner varios ejemplos:

• El límite de la sucesión de $B_n = \overline{B}((0,0),1/n)$, la bola cerrada de centro el origen y radio $1/n$, es igual al punto $(0,0)$. Esto es natural ya que este límite coincide con el límite en conjuntos: es una sucesión monótona decreciente de conjuntos, así que su límite coincide con la intersección de todos ellos, que es el origen.

• Un ejemplo parecido es $C_n = C((0,0), 1/n)$, en este caso las circunferencias de centro origen y radio $1/n$. El límite bajo la distancia de Hausdorff sigue siendo el punto origen (se puede ver fácilmente que la distancia de Hausdorff entre el origen y $C_n$ es exactamente $1/n$ que converge a $0$), pero esta vez el límite como conjuntos sería el vacío.

Que los conjuntos compactos del plano tengan una distancia ya implica que forman un espacio métrico, que podemos tomar límites cuando existan y que estos límites son únicos porque todo espacio métrico es un espacio $T_2$. La pregunta natural es, ¿cuál es la función que tiene como gráfica el límite de las gráficas de una sucesión $f_n$?

Primero tenemos que especificar que exista al menos una función. Hay ciertos ejemplos, como el primero del que hemos hablado, cuyo límite de gráficas no es una función ya que existe una recta vertical que corta al límite en más de un punto.

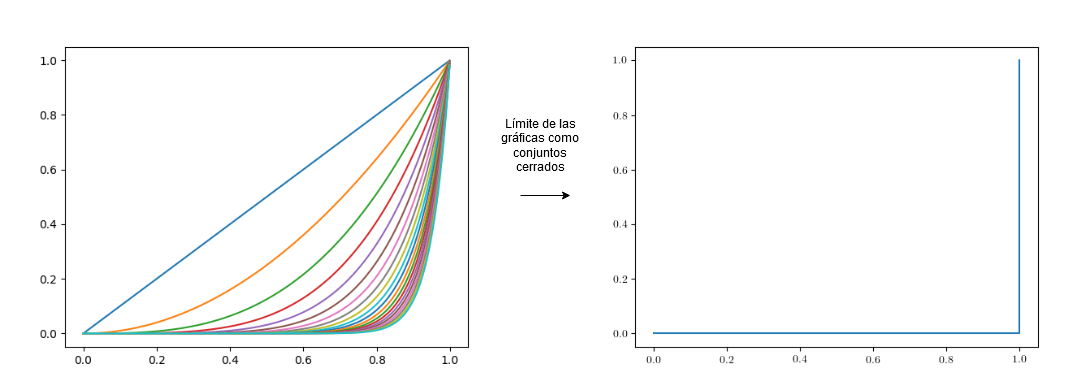
En el caso de que $A$ sea compacto, os voy a probar que el límite inducido por la distancia de Hausdorff en funciones continuas es equivalente a la convergencia uniforme, bajo la restricción anterior de que el límite pertenezca a la gráfica de alguna función. Hay una razón geométrica bastante sencilla de este hecho, que tiene relación con los entornos tubulares formados por la curva de la función. Para motivaros un poco antes de empezar a hacer cuentas, os voy a poner este ejemplo.

Cuando hablamos de convergencia uniforme, esta convergencia está asociada a la norma uniforme, es decir, la norma del supremo: $\lVert f \rVert_\infty = \sup_{x\in A} \|f(x)\|$. Pensad en cuáles son las bolas abiertas de centro $f$ y radio $r$ en este espacio. Son el conjunto de funciones cuya gráfica está encerrada entre $f-r$ y $f+r.$

Por otro lado, en la distancia Hausdorff no podemos hablar de bolas abiertas en el espacio de las funciones, tenemos que volver al espacio de las gráficas. Así que la pregunta es cómo son las bolas abiertas de centro la gráfica de $f$ y radio $r$. Son el conjunto de funciones cuya gráfica está a una distancia menor o igual a $r$ con la de $f$. Si habéis estudiado o leído geometría de curvas, igual os suena que estas curvas se llaman curvas paralelas. Podéis crear las curvas paralelas a distancia $r$ (plural porque es posible que haya dos) de una dada si en cada punto se dibuja la circunferencia de radio $r$, la curva paralela está formada por una que es tangente a todas estas circunferencias, también llamada la envolvente de esta familia de circunferencias. Aunque la envolvente suele ser bastante difícil de calcular, en este caso si la curva original es diferenciable podéis parametrizar las curvas paralelas fácilmente.

Vamos a dibujar un ejemplo de ambas bolas. Cogemos como función la semicircunferencia superior de centro origen y radio $1$ en $A=[-1,1]$, es decir, $f(x) = \sqrt{1-x^2}$, y buscamos las funciones que estén a distancia $1/2$ en ambas distancias:

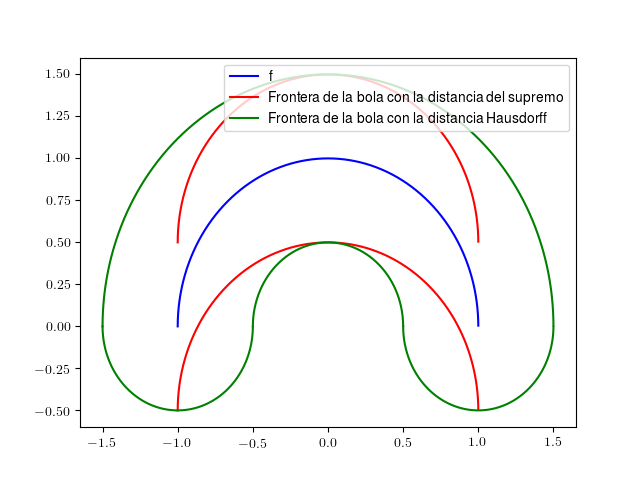
Las funciones cuya gráfica se queda contenida en el conjunto delimitado por la curva verde son las que forman la bola en la distancia de Hausdorff. Por otro lado, las funciones definidas en $[-1,1]$ cuya gráfica se queda por debajo de $f+1/2$ y por encima de $f-1/2$, las curvas rojas, son las que forman la bola bajo la distancia del supremo, o norma uniforme. Un conjunto lo forman las circunferencias de radio $r$ y el otro lo forman segmentos verticales de longitud $r$, así que no sería extraño que ambos provocaran límites equivalentes.

De hecho, mirando el ejemplo podemos visualizar una propiedad que vamos a usar en la demostración. Parece que la bola con la distancia Hausdorff contiene a la bola con la norma uniforme. Esto se debe a que la distancia de Hausdorff es menor o igual que la distancia de la norma del supremo. En efecto, sean $f,g:A \rightarrow \mathbb{R}$ funciones continuas con gráficas $F,G \subset \mathbb{R}^2$ respectivamente:

$$d_\infty(f,g) = \sup_{x\in A} \| f(x)-g(x)\| = k \Rightarrow$$ $$\Rightarrow \forall x \in A ~ d(f(x), G) \leq k \wedge d(F, g(x)) \leq k \Rightarrow$$ $$\Rightarrow d_H(F,G) \leq k = d_\infty(f,g)$$

Como la distancia de Hausdorff entre $F$ y $G$ es menor o igual a la distancia de $d_\infty$, se tiene que la bola de Hausdorff debe ser mayor o igual que la bola con la distancia uniforme, así que la contiene. Esta propiedad implica que toda sucesión $f_n$ que converja uniformemente a $f$ cumple que las gráficas $F_n$ convergen a $F$ bajo la distancia de Hausdorff. Es decir, todo límite en convergencia uniforme implica convergencia de gráficas. La demostración es sencilla: $d(F_n, F) \leq d_\infty(f_n, f) \rightarrow 0$.

Para terminar veamos la otra implicación. Sea $A\subset \mathbb{R}$ un conjunto compacto, y supongamos $f_n : A\rightarrow \mathbb{R}$ funciones continuas con gráficas $F_n$, para cada $n\in \mathbb{N}$, tales que existe una función $f$ con gráfica $F$ y $F_n \rightarrow F$ como conjuntos compactos en el plano. Entonces $\{f_n\}_{n\in \mathbb{N}}$ converge uniformemente a $f$.

Demostración: $f_n$ son continuas en un conjunto compacto así que son uniformemente continuas, lo que significa que $\forall \epsilon > 0 ~ \exists \delta > 0$, podemos suponer que $\delta < \epsilon$, tal que $\forall x,y \in A$ con $\vert y-x\vert < \delta \Rightarrow \vert f(y)-f(x) \vert < \epsilon$.

Por otro lado, la condición de que $F_n$ converge a $F$ significa que $\forall \epsilon > 0 ~ \exists N \in \mathbb{N}$ tal que $\forall n\geq N ~ \forall x \in A ~ d(f_n(x), F) \leq \epsilon \wedge d(f(x), F_n) \leq \epsilon$. Así que sea $\epsilon > 0$, tomamos $\delta > 0$ de la continuidad uniforme. Ahora aplicamos con $\delta/2$ la condición del límite, existe $N$ tal que para todo $n \geq N$ se tiene que la distancia entre $F_n$ y $F$ es menor que $\delta/2$.

Sea $s_n(x) = \vert f_n(x) - f(x) \vert$, nuestro objetivo es probar que $\sup s_n(x) \rightarrow 0$. Vamos a hacer un esbozo, para un valor de $x\in A$ particular, cuánto vale $s_n(x)$ para $n \geq N$, donde tenemos que la distancia entre gráficas $F_n$ y $F$ es menor que $\delta/2$.

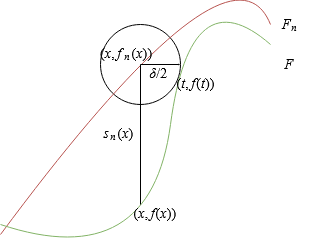
Formalmente, tomamos el punto de $(t,f(t)\in F$ más cercano a $(x,f_n(x))$, sabiendo que la distancia entre ambos puntos es menor o igual a $\delta/2$. Esto implica que:

$$s_n(x) \leq \delta/2 + \vert f(t)-f(x)\vert,$$

y utilizando la continuidad uniforme, debido a que $\vert t - x\vert \leq \delta/2 < \delta \Rightarrow \vert f(t)-f(x)\vert < \epsilon$, así que:

$$s_n(x) \leq \delta/2 + \epsilon < 2\epsilon.$$

Como este proceso lo hemos realizado para cualquier $x\in A$, se tiene que $\sup s_n(x) \leq 2\epsilon$, así que hemos demostrado que para todo $\epsilon > 0$ existe $N\in \mathbb{N}$ tal que para todo $n \geq N$ se tiene que $\sup s_n(x) \leq 2\epsilon$, lo cual prueba que $\sup s_n(x) \rightarrow 0$ y por tanto, $f_n$ converge uniformemente a $f$.

Así que, en funciones continuas en compactos tomar convergencia uniforme es equivalente que tomar convergencia de sus gráficas. Me parece un resultado bastante gracioso, relativamente sencillo de probar y aunque sea inútil, a partir de ahora siempre podéis decir que podéis tomar el límite dibujando las gráficas para molestar a quienes digan que los dibujos no demuestran nada.